1장 union Find
▶Contents
- Union Find
- Quick Find
- Quick Union
▶Union Find
- N개 객체가 주어진다.
- 0 ~ (N-1)까지 정점(vertex)으로 표현된다.
- 간선(edge)이 없는 상태에서 시작한다.
- 2개의 명령 수행이 필요하다.
- Union(a, b) : 점 a와 b를 간선으로 연결
- Connected(a, b) : a와 b를 연결하는 경로 존재하는지 True/False로 응답한다. (Find라고도 한다.)
- 값이 Union 됨에 따라서 Connected(Find) 값이 달라진다.
- 한마디로 연결 상태가 동적으로 계속 변한다. (그때그때 다시 답을 확인할 필요가 있다.)
- union(a, b), connected(a, b)를 수행하려면 그래프 연결 상태를 저장할 필요가 있다.
- Adjacency list 방식 : adj[v]에 v에 인접한 정점 목록을 저장
- union(a, b) : O(1) 상수 시간에 해결 가능하다.
- connected(a, b) : 그래프가 커지면 비효율적이다. O(E 간선의 개수)
- 경로를 찾거나, 간선을 삭제할 경우에는 개별 간선 정보가 꼭 필요하다.
- connected component에 속하는지 계속 기록하고 업데이트한다.
- connected component : 서로 연결된 정점들의 maximal한 집합
- ids[]를 사용해 각 객체가 어느 connected component에 속하는지 기록한다
- ids[i] : 객체 i가 속한 component의 id
- id : 서로 다른 component에 서로 다른 숫자 부여한다. 속한 객체 중 가장 작은 번호를 사용한다.
- Adjacency list 방식 : adj[v]에 v에 인접한 정점 목록을 저장
▶Quick Find
- ids[]를 사용해 각 객체가 어느 connected component에 속하는지 기록한다.
- ids[i] : 객체 i가 속한 component의 id
- id : 서로 다른 component에 서로 다른 숫자 부여한다. 속한 객체 중 가장 작은 번호를 사용한다.

- Q. 왜 이렇게 저장하는 가?
- A1. Connected(a, b)를 빠르게 할 수 있음. 그래서 Quick Find라고 부른다.
- A2. N x N 배열이나 adj_list를 사용해 개별 간선 정보를 일일이 저장하지 않아도 된다.
- 1 x N 배열에 필요한 정보를 다 담을 수 있다.
ids[i] = i로 초기화
def connected(a,b):
return (ids[a] == ids[b])
def union(a,b):
ids[i] == ids[b]인 모든 i에 대해 ids[i] = ids[a]로 값 교체
#혹은
ids[i] == ids[a]인 모든 i에 대해 ids[i] = ids[b]로 값 교체위에 간단한 슈도코드를 아래의 코드로 바꿔서 작성하였습니다.
N = 8
ids = []
for idx in range(N):
ids.append(idx) # 정점 번호로 ids[] 초기화
def connected(p, q):
return ids[p] == ids[q]
def minMax(a, b):
if a<b: return a,b
else: return b,a
def union(p, q):
id1, id2 = minMax(ids[p], ids[q])
for idx, _ in enumerate(ids):
if ids[idx] == id2: ids[idx] = id1| Algorithm | ids[] 초기화 | union | find(connected) |
| Quick-Find | O(N) | O(N) | O(1) - 상수시간 |
▶Quick Find에서 사용하던 구조의 다른 해석
- connected component를 tree로 본다.
- ids[i] : 객체 i의 parent
- 만약 객체 i가 root라면 ids[i] = i
- connected(p, q) == True if root(p) == root(q)
- union(p, q) : p가 속한 tree 상의 모든 node를 q가 속한 tree 아래로 옮겨 붙이기.

▶Quick Union
- connected(p, q) == True if root(p) == root(q)
- root(i) = ids[ids[ids[… ids[i] …]]
- root를 찾으려면 계속해서 타고 올라가야 한다.
- union(p, q) : root(p)를 root(q) 아래로 옮겨 붙이기.

N = 10
ids = []
for idx in range(N): # ids 초기화
ids.append(idx)
def root(i):
while i != ids[i]: i = ids[i]
return i
def connected(p, q):
return root(p) == root(q)
def union(p, q):
id1, id2 = root(p), root(q)
ids[id1] = id2union 할 때마다 root를 찾아야 한다. (O(d) -> 트리의 길이)
| Algorithm | ids[] 초기화 | union | find(connected) |
| Quick-Find | O(N) | O(N) | O(1) |
| Quick-Union | O(N) | O(N) | O(N) |
트리가 커지면 깊이가 깊어져서 Quick-Union 할 때 find, union 하는 시간이 오래 걸린다.
▶Weighted Quick Union - QU에서 트리 깊이 제한
- union(p, q) : 작은 트리의 root를 큰 트리의 root 아래에 연결한다.
- union후에 depth는 증가하지 않는다.
- 만약 두 tree의 크기가 같다면 그때는 depth가 1 증가한다.
N = 10
ids = []
size = [] # size[i]: size of tree rooted at i
for idx in range(N):
ids.append(idx)
size.append(1)
def root(i):
while i != ids[i]: i = ids[i]
return i
def connected(p, q):
return root(p) == root(q)
def union(p, q):
id1, id2 = root(p), root(q)
if id1 == id2: return #이미 연결
if size[id1] <= size[id2]: #p가 속한 트리의 사이즈가 작은 경우
ids[id1] = id2
size[id2] += size[id1]
else: #q가 속한 트리의 사이즈가 작은 경우
ids[id2] = id1
size[id1] += size[id2]- 어떤 객체 x의 깊이도 ≤ log2 (N)으로 제한된다.
- 증명
- N개 객체 중 임의의 정점을 x라 하자.
- x의 깊이가 +1 될 때는 x가 속한 트리가 (작아서) 더 큰 트리에 연결될 때
- 이때 x가 속한 tree의 크기는 최소 2배가 된다.
- 그런데 이렇게 크기가 2배가 되는 것은 많아봐야 log2 (N) 회
- x의 깊이가 k번 +1 된다고 가정하면,
- x가 속한 트리의 크기는 최소 2^k
- 전체 그래프에 N개의 객체만 있으므로 2^k ≤N
- 따라서 k ≤ log2 (N)
| Algorithm | ids[] 초기화 | union | find(connected) |
| Quick-Find | O(N) | O(N) | O(1) |
| Quick-Union | O(N) | O(N) | O(N) |
| Weight QU | O(N) | O(log(N)) | O(log(N)) |
2장 sorting(shell sort,shuffle sort,convex hull)
▶Contents
- Insertion Sort
- h-Sort
- Shell Sort
- Shuffle Sort
- Convex Hull (Tight boundarry 찾기 위해 정렬 방법 적용)
▶Insertion Sort
- 이미 정렬된 a[0] ~ a[i-1]에 a[i]를 적절한 위치 (정렬되었을 때의 위치) 찾아 추가한다.
- 그 결과 a[0] ~ a[i]까지 정렬된 상태가 된다.
| 입력 데이터의 상태 | 대소 비교 횟수 | swap 횟수 |
| (best case) 이미 정렬된 상태 | N - 1 | 0 |
| (worst case) 반대 방향으로 정렬된 상태 | ~N^2 / 2 | ~N^2 / 2 |
| (average case) 각 원소를 절반 정도 이동시켜야 하는 상태 |
~N^2 / 4 | ~N^2 / 4 |
▶h-Sort
- 모든 h만큼 떨어진 원소끼리 정렬된 상태로 만든다.
- 이때 insertion sort방식을 이용한다.
- Shell Sort에서 사용하는 기본 operation이 h-Sort이다.

def hInsertionSort(a, h):
for i in range(h, len(a)):
key = a[i]
j = i-h
while j>=0 and a[j] > key:
a[j+h] = a[j]
j -= h
a[j+h] = keydef insertionSort(a):
for i in range(1, len(a)):
key = a[i]
j = i-1
while j>=0 and a[j] > key:
a[j+1] = a[j]
j -= 1
a[j+1] = keyh-sort와 insertion sort를 비교해보면,
insertion sort는 1칸씩 이동하는데 h-sort는 h칸씩 이동하면서 비교한다.
최종적으로는 1-sort를 수행해 완전히 정렬된 상태로 만들어야 한다.
- h-sort에서 h값은 어떻게 선정해야 하나?
- 2^k : 1 ← 2 ← 4 ← 8 ← 16 ← 32 ← ...
- 홀짝끼리 각각만 정렬되기에 좋지 않다.
- 2^k - 1 : 1 ← 3 ← 7 ← 15 ← 31 ← 63 ← ...
- 2^k와 같은 문제는 없다.
- 3x + 1 : 1 ← 4 ← 13 ← 0 ← 121 ← 364
- Donald Knuth가 제안한 방법
- 다음 h를 계산하기 쉬운 편이며, 성능도 괜찮다.
- 1 ← 5 ← 19 ← 41 ← 109 ← 209 ← ...
- R.Sedgewick 교수가 제안한 방법
- 지금까지 보인 수열 중에 성능이 가장 나은 편이다.
- 2^k : 1 ← 2 ← 4 ← 8 ← 16 ← 32 ← ...
▶Shell Sort
def shellSort(a):
N = len(a)
h = 1
while h < N/3:
h = 3*h + 1 # Knuth's Sequence 1, 4, 13, 40, ...
while h >= 1:
hInsertionSort(a, h)
h = h//3- Shell Sort의 성능 분석: 아직 정확한 수학적 모델을 찾지는 못했다.
- 각 h-sort가 실험적으로 ≤ cN회 (c는 작은 정수) 비교/swap 하는 걸로 보였으나 정확한 수학적 모델은 찾지 못했다.
- h = 3x + 1을 사용하는 경우 ~logN 회의 h-sort 수행한다.
- 따라서 ~NlogN 회의 비교/swap을 수행할 것으로 예측된다.
▶Shuffle Sort
- Shell Sort
import random
def shuffleSort(a):
# Generate a random real number for each entry in a[]
r = []
for _ in range(len(a)):
r.append(random.random())
# Sort according to the random real number
return [i for i, _ in sorted(zip(a,r), key=lambda x: x[1])]
- Knuth's Shuffle
- Iteration i 때 a[0]~a[i] 중 하나를 uniformly random 하게 선정해 a[i]와 swap
- 그 결과 a[0] ~ a[i]가 uniformly random 하게 shuffle 된 상태이다.
import random
def knuthShuffle(a):
for i in range(1, len(a)):
j = random.randint(0,i) # Randomly select a position among 0 ~ i
a[i], a[j] = a[j], a[i] # Swap a[i], a[j]
▶Convex Hull
- Convex (볼록한) Hull (껍데기) of a set of N points:
- 집합의 꼭짓점이 점인 모든 주어진 점을 덮는 가장 작은 다각형

- convex hull 활용 예
- Robot Motion Planning
- Polygon(다각형) 형태 장애물 있을 때 두 지점 s와 t 간 최단 경로 찾기
- Farthest Pair 찾기
- 평면 상에 N개의 점이 있을 때, 서로 거리가 가장 먼 두 점 찾기
- Robot Motion Planning
- convex hull에 대해 알아야 할 성질
- 반시계 방향 순서로 포함할 점 선택
- 최저점과 각도 순으로 선택
- y값이 가장 작은 점을 p라고 둔다.
- p로부터의 각도가 증가하는 순으로 점을 골라서 파악한다.
첫 번째 방법 : 반시계 방향 turn 반복 + 각도 순으로 선택
y값 가장 작은 점 p에서 시작해 반시계 방향 각도 가장 작은 점으로 연결
마지막에 a → b 순서로 선택했다면 b로부터 a-b 라인과 반시계 방향 각도 가장 작은 점으로 연결

두 번째 방법 : Graham's Scan
y값 가장 작은 점 p에서 시작해 다른 모든 점과의 반시계 방향 각도 계산
각도가 작은 점 순으로 차례로 연결해 보며 새로운 점 연결할 때마다 아래 수행
마지막에 i→j→k 순으로 연결했다면 i-j선 기준으로 볼 때 j-k가 반시계 방향의 turn이 아니라면
(즉 i-j-k가 convex 아닌 concave angle을 만든다면)
j는 잘못 연결된 것으로 보고 convex hull에서 제외 (즉 i-k 직접 연결)
더는 제외할 점 없을 때까지 마지막 세 점의 concave 여부 확인 반복

▶정리 : Sort & Applications
- Shell Sort
- Insertion Sort를 넓은 간격 → 좁은 간격 순서로 적용함으로써 성능을 향상시킨 예
- Shuffle
- 원소 수만큼 난수 발생 후 Sort
- Insertion Sort와 유사한 방식으로 한 원소 씩 추가해 가되, 랜덤한 위치에 추가
- Convex Hull
- Sort를 활용해 tight한 boundary 찾기
- 이들은 Sort를 직접 활용하거나, Sort와 유사한 방법 활용하며 Sort의 성능이 방법의 성능에 큰 영향 미친다.
3장 Sorting (merge Sort,Quick sort)
▶Contents
- Bottom-up Merge Sort
- Sorting Complexity
- Stability of Sorting
- Quick Select
- Duplicate Keys and 3-way Partitioning
▶Merge Sort
인접한 두 조각끼리 Merge(정렬된 순서로 병합)을 반복한다.
총 N개 원소를 병합한다면, 이들을 순서에 맞게 차례로 결과 배열에 옮겨 담으므로 ~N회 작업이 필요하다.
이러한 작업을 ~log(N)회 반복해야 한다.
입력 데이터 크기가 N이라면 결과를 옮겨 담을 ~N의 추가 공간도 필요하다.
# Halve a[lo ~ hi], sort each half and merge,
# using the extra space aux[]
def divideNMerge(a, aux, lo, hi):
if (hi <= lo):
return a
mid = (lo + hi) // 2
divideNMerge(a, aux, lo, mid)
divideNMerge(a, aux, mid+1, hi)
merge(a, aux, lo, mid, hi)
def mergeSort(a):
# Create the auxiliary array once and
# re-use for all subsequent merges
aux = [None] * len(a)
divideNMerge(a, aux, 0, len(a)-1)배열을 나누어가는 과정에서 재귀를 계속해서 호출한다.
-> 시간/공간 overhead가 크다.
이를 해결한 방법이 Bottom-up Merge Sort이다.
Divide 하기 위해 재귀 호출하는 과정을 생략했다. 아래 표와 같이 merge만 수행한다.
sz = 1에서 시작하고, 크기 sz인 인접한 부분끼리만 병합한다.
다음 sz를 2배 해주고 sz >= N 될 때까지 반복한다.
(auz는 ~N 크기의 추가 공간이다.)


<merge 코드 - Bottom-up version에서도 그대로 사용>
# Merge a[lo ~ mid] with a[mid+1 ~ hi],
# using the extra space aux[]
def merge(a, aux, lo, mid, hi):
# Copy elements in a[] to aux[]
for k in range(lo, hi+1):
aux[k] = a[k]
i, j = lo, mid+1
for k in range(lo, hi+1):
if i>mid: a[k], j = aux[j], j+1
elif j>hi: a[k], i = aux[i], i+1
elif aux[i] <= aux[j]: a[k], i = aux[i], i+1
else: a[k], j = aux[j], j+1정렬된 조각 1(a[lo] ~ a[mid])과 정렬된 조각 2(a[mid + 1] ~ a[hi])를 병합한다.
aus는 ~N 크기의 추가 공간이다.
<재귀 호출하는 Top-down version>
# Halve a[lo ~ hi],
# sort each of the halves,
# and merge them,
# using the extra space aux[]
def divideNMerge(a, aux, lo, hi):
if (hi <= lo):
return a
mid = (lo + hi) // 2
divideNMerge(a, aux, lo, mid)
divideNMerge(a, aux, mid+1, hi)
merge(a, aux, lo, mid, hi)
def mergeSort(a):
# Create the auxiliary array once
# re-use for all subsequent merges
aux = [None] * len(a)
divideNMerge(a, aux, 0, len(a)-1)
<Bottom-up version merge sort>
def mergeSort(a): 11
# Create the auxiliary array
aux = [None] * len(a)
sz = 1
while(sz<len(a)):
for lo in range(0, len(a)-sz, sz*2):
merge(a, aux, lo, lo+sz-1, min(lo+sz+sz-1, len(a)-1))
sz += sz # Multiply by 2Q. merge함수 마지막 인자에 min() 함수를 사용한 이유는?
A. 1, 2, 4, 8...로 진행하는데, 배수로 떨어지지 않을 수도 있기 때문이다.
Q. for(lo = 0; lo < len(a) - sz; lo += sz * 2)에서 lo < len(a) - sz를 한 이유는?
A. 잘 모르겠다.
▶Sorting Complexity
Q. 과연 정렬 알고리즘은 얼마나 빨라질 수 있을까?
A. 최적의 알고리즘을 찾기 위해, 혹은 더 개선할 여지를 발견하기 위해서 노력 중이다.
Q. Merge Sort, Quick Sort는 최적의 속도에 다다랐는가?
A. NlogN까지는 가능하다.
임의의 N개를 대소 비교해 나온 모든 경우의 수에 대해서 일반화해보자.
Q. 깊이가 h인 이진 트리에는 (한번 분기했을 때 깊이가 1이 된다고 가정) 잎이 최대 몇 개인가?
A. 한번 하면 잎의 개수가 2개
2번 하면 (깊이는 2) 2^2 = 4개
...
h번하면 (깊이는 h) 잎의 개수 <= 2^h
=이 아닌 <=인 이유는 빠르게 결괏값이 나오면 더 이상 구분을 안 하기 때문이다.
Q. N개 원소에 대한 모든 가능한 정렬이 잎에 한 번은 나오려면, 잎이 최소 몇 개 있어야 하나?
A. N개의 원소이면 N! 가지가 나오기 때문에 잎의 개수는 N! 보다 크다.
위의 문제와 비교 합치면 N! <= 잎의 개수 <= 2^h이다.
따라서 N! <= 2^h가 된다.
Q. 앞 두 문제의 답으로부터 N(정렬할 원소 개수)과 h(worst-case 비교 횟수) 간 관계를 구해보자.
A. N! <= 2^h
log2 N! <= h = 비교 횟수
log2 N! = log2 (N * (N-1) *... * 1)
= log2 N +... + log2 1
<= log2 N +... + log2 N
= Nlog2 N
따라서 비교 횟수 h는 NlogN이 된다.
N개의 서로 다른 원소가 있는 경우, 최적의 정렬 방법은 ~NlogN회 대소 비교가 필요하다.
merge sort(worst case), quick sort(average case)는 이러한 최저치에 가깝다.
▶Stability of Sorting : 정렬 시 추가로 만족시켜야 할 성질
key : 여러 값으로 이루어진 원소의 경우 (예 : class 객체) 정렬에 사용하는 값
정렬 전후 key가 같은 원소 간 상대 순서 보존하는 성질
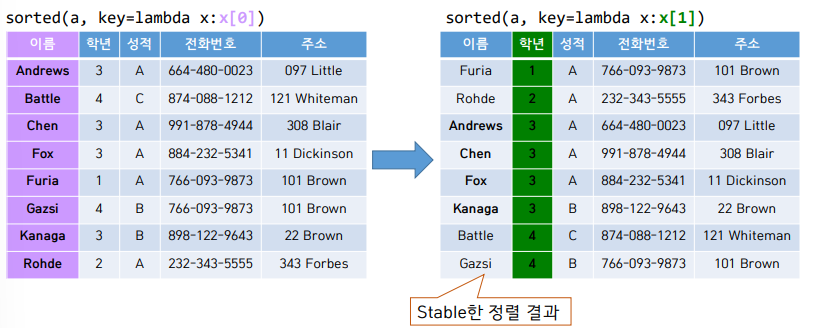
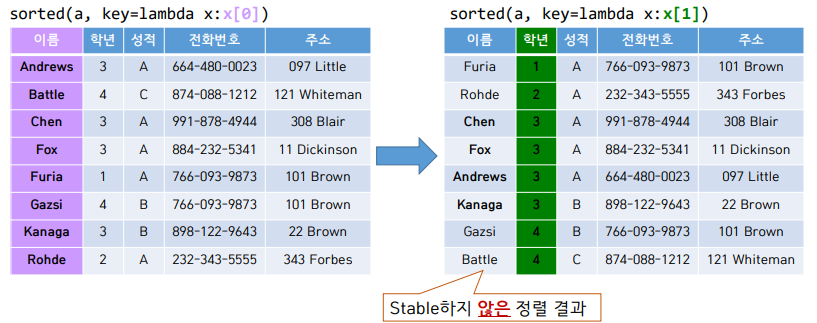
Insertion Sort는 Stable 하다.
iteration i에 이미 정렬된 a[0] ~ a[i-1]에 a[i]를 적절한 위치 (정렬되었을 때의 위치) 찾아서 추가한다.
그 결과 a[0] ~ a[i]까지 정렬된 상태가 된다.

def insertionSort(a):
for i in range(1, len(a)):
key = a[i]
j = i-1
while j>=0 and a[j] > key:
a[j+1] = a[j]
j -= 1
a[j+1] = keyQ. a[j] >= key로 수정해도 stable한가?
A. stable하지 않다.
왜냐하면 같은 E여도 먼저 들어온 E의 위치는 건들면 안 된다.
>=로 하면 E1과 E2는 같기 때문에, 서로 자리가 바뀌게 된다.
그렇기 때문에 stable하지 않게 된다.
Selection Sort는 Stable하지 않다.
iteration i에 a[i] ~ a[N - 1] 중 최솟값을 찾아 a[i]와 swap 해준다.

def selectionSort(a):
for i in range(len(a)-1):
# Find the minimum in a[i]~a[N-1]
min_idx = i
for j in range(i+1, len(a)):
if a[j] < a[min_idx]:
min_idx = j
# Swap the found minimum with a[i]
a[i], a[min_idx] = a[min_idx], a[i]코드의 마지막 부분, 서로 자리를 바꾸는 코드 때문에 stable하지 않게 되는 것이다.
원거리 swap을 하기 때문이다.
가장 작은 값을 앞으로 당겨서 넣는데 그 자리에 B1이 있으면 B1이 뒤로 갈 수 있기 때문이다.
Shell Sort는 Stable하지 않다.
h를 점진적으로 1까지 감소시켜가면서 h-sort를 수행한다.
shell sort는 selection sort의 코드를 가져와 일부 수정해서 만든 것이다.
그렇기에 selection sort처럼 원거리 swap을 하기 때문에 stable하지 않다.
ex. 4-sort : C1 B1 B2 B3 B4 -> B4 B1 B2 B3 C1
ex. 4-sort : B1 B2 B3 B4 A1 -> A1 B2 B3 B4 B1
Merge Sort는 Stable 하다.
크기가 1인 조각에서 시작해 인접한 조각끼리 merge 한다.
# Merge a[lo ~ mid] with a[mid+1 ~ hi],
# using the extra space aux[]
def merge(a, aux, lo, mid, hi):
# Copy elements in a[] to aux[]
for k in range(lo, hi+1):
aux[k] = a[k]
i, j = lo, mid+1
for k in range(lo, hi+1):
if i>mid:
a[k], j = aux[j], j+1
elif j>hi:
a[k], i = aux[i], i+1
elif aux[i] <= aux[j]:
a[k], i = aux[i], i+1
else:
a[k], j = aux[j], j+1코드 13번째 줄에서 <=를 <로 바꾸면 stable 하지 않게 된다.
두 개의 조각을 합쳐야 한다. 왼쪽에 있는 조각이 i를 기준으로, 오른쪽 조각이 인덱스 j부터이다.
만약 i번째와 j번째가 같으면 원래는 i를 집어넣는다.
하지만 <=를 <로 바꾸면 그 코드를 하지 않고 j를 넣는 코드를 하기 때문에, 뒤에 것이 들어가 stable이 깨진다.
Quick Sort는 Stable하지 않다.
# Partition a[lo~hi] using a[lo] as pivot
def partition(a, lo, hi):
i, j = lo+1, hi
while True:
while i<=hi and a[i]<a[lo]:
i = i+1
while j>=lo+1 and a[j]>a[lo]:
j = j-1
if (j <= i):
break # Pointers cross
a[i],a[j] = a[j],a[i] # Swap(a[i],a[j])
i,j = i+1,j-1
a[lo],a[j] = a[j], a[lo] # Swap a[j] with pivot
return j # Return the index of item in place첫 값을 기준으로 작은 값과 큰 값을 구분한다.
그럼 순서에서 첫 값, 작은 값들, 큰 값들이 된다.
다음으로 첫 값을 사이에 넣어서 작은 값, 첫 값, 큰 값들로 구성한다.
처음에 첫 값을 기준으로 구분할 때 원거리 swap을 하게 된다.
뒤에서부터 먼저 나온 작은 값과, 앞에서부터 나온 큰 값이 교환하게 된다.
그럼 작은 값과 같은 값이 중간에 나오게 되면, 순서가 꼬이게 된다.
정렬의 stability는 많은 application에서 중요하다.
merge sort는 효율적일 뿐 아니라 (worst case ~NlogN) stable 해서, 'stability' 요구하는 application에서는 quick sort보다 선호된다.
▶Quick Select
Quick sort
v를 기준 값으로 좌우로 partition후 각 조각을 다시 partition 하는 방식이다.
partition 했을 때 기분 값은 정렬된 위치에 있게 된다.
N=2개의 원소를 partition 하면 정렬이 완료되므로, 좌우 조각을 partition 하다 보면 모든 원소가 정렬된다.

Selection
크기 N의 배열이 주어졌을 때, k번째로 작은 원소 찾기이다. (k는 0부터 시작이다.)
0 <= k <= N-1
k = 0인 경우 : 최솟값(min) 찾기
k = N - 1인 경우 : 최댓값(max) 찾기
k = N / 2인 경우 : 중간값(median) 찾기
quick sort의 방식을 사용하면 된다.
quick sort는 기준 값을 가지고 좌우를 다 partition 하는 방식이라면,
quick select는 원하는 방향만 partition 해주면 된다.
partition 하면 기준 값 a[j]는 정렬된 위치에 있다.
j == k라면 k번째 원소를 찾았기 때문에 a[j]를 반환해준다.
j < k라면 오른쪽 partition만 분할해준다.
j > k라면 왼쪽 partition만 분할해준다.

<Quick Sort 코드>
# Partition a[lo~hi] and
# continue to partition each half recursively
def divideNPartition(a, lo, hi):
if (hi <= lo): return
j = partition(a, lo, hi)
divideNPartition(a, lo, j-1)
divideNPartition(a, j+1, hi)
# 양쪽 partition 모두 다시 분할한다.
# 둘 이상 가지로 분기하므로 재귀 호출로 작성하면 편하다.
def quickSort(a):
# Randomly shuffle a,
# so that the partitioning item is chosen randomly
random.shuffle(a)
divideNPartition(a, 0, len(a)-1)
<Quick select 코드>
# Find k-th smallest element,
# where k = 0 ~ len(a)-1
def quickSelect(a, k):
# Randomly shuffle a, so that two
# partitions are equal-sized
random.shuffle(a)
lo, hi = 0, len(a)-1
while (lo < hi):
j = partition(a, lo, hi)
if j<k:
lo = j+1
elif k<j:
hi = j-1
else:
return a[k]
return a[k]배열 a를 shuffle 해야 더 균등하게 분할해서 성능이 좋다.
Quick Select의 성능
N개의 값 partition 위해서 N에 비례한 횟수의 비교/메모리 접근을 수행한다.
N개의 원소를 크기 1이 될 때까지 대략 반으로 나누어간다면,
N + N/2 + N/4 +... + 1 = ~2N에 비례한 횟수의 비교/메모리 접근을 수행한다.
N개의 원소를 partition 해서 크기 N-1인 조각이 계속해서 나오는 경우,
N + N-1 + N-2 +... + 1 = ~n^2 / 2에 비례한 횟수의 비교/메모리 접근을 수행한다.
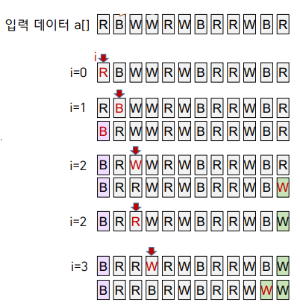
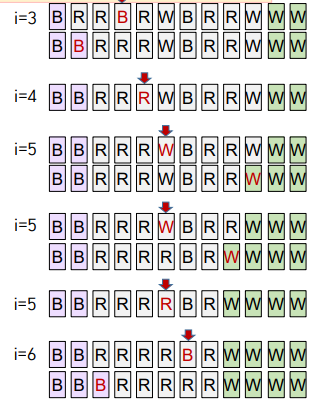
3-Way Partitioning
a[low ~ hi]를 3-way partition 하기 위해 a[low]를 기준 값 v로 정한다.
최종적으로 3개 영역으로 나누고자 한다.
1. 왼쪽→오른쪽 방향으로 한 번에 한 원소 a[i] 검사한다.
2. a[i] < v이면(기준값 보다 작다.) 왼쪽 영역(의 오른쪽 끝 - lt)으로 이동한다.(swap) i++
3. a[i] > v이면(기준값 보다 크다.) 오른쪽 영역(의 왼쪽 끝 - gt)으로 이동한다.(swap)
4. a[i]==v 이면 이동시키지 않는다. i++
5. i가 오른쪽 영역에 들어서면 검사 중단한다.
Q. v보다 작은 값을 왼쪽 영역으로 이동시킬 때는 i++하지만 큰 값을 오른쪽으로 이동시킬 때는 i++하지 않는 이유는?
A. 오른쪽에 있는 값중에서 gt로 지정한 부분을 앞으로 가져오기 때문이다.
그 값은 아직 비교하지 않은 값이기 때문에, 그대로 i값을 가지고 v와 비교해주어도 되기 때문이다.
하지만, v보다 작은 값을 이동시키게 되면, swap 해줄 때 이미 비교한 값과 자리를 바꿔주게 된다.
그렇기 때문에 그때는 i++을 해주어 다음 값으로 v와 비교를 진행해야 한다.
def partition3Way(a, lo, hi):
if (hi <= lo):
return
v = a[lo]
lt,gt = lo,hi # Pointers to <v and >v sections
i = lo
while i <= gt:
if a[i] < v:
a[lt], a[i] = a[i], a[lt] # Swap
lt, i = lt+1, i+1
elif a[i] > v:
a[gt], a[i] = a[i], a[gt] # Swap
gt = gt-1
else: i = i+1
print(a)
partition3Way(a, lo, lt-1)
partition3Way(a, gt+1, hi)
3-Way Quick Sort 성능
N개 원소 중 n개 서로 다른 key가 있고 i번째 key가 xi개 존재한다면 다음과 같은 횟수의 작업 필요하다.
ex. x1이 5개, x2가 6개, x3가 7개, 총 N이 18개면
-5 * log(5 / 18) -6 * log(6 / 18) -7 * log(7 / 18)이 된다.
모든 key가 다 다르면 (N개 key가 한 번씩 나오는 경우) : ~NlogN
n개 key가 N/n번씩 나온다면 : ~Nlogn
따라서 n이 작아질수록 (duplicate key가 많을수록) ~N에 가까워진다.
정리: Merge Sort, Quick Sort, 개선점, Applications
| Merge Sort | Quick Sort | 3-way Quick Sort | ??? | |
| 방법 | 작은 조각 -> 큰조각 순으로 merge 하면서 정렬 | 큰 조각 -> 작은 조각 순으로 partition 하면서 정렬 | 3조각으로 분할 후 왼쪽, 오른쪽 조각만 이어서 분할 | |
| Best | NlogN | NlogN | N | N |
| Average | NlogN | NlogN | NlogN | NlogN |
| Worst | NlogN | N^2 / 2 | N^2 / 2 | NlogN |
| 추가 공간 필요? | ~N 추가 공간 필요 | 불필요 | 불필요 | 불필요 |
| Stable | Yes | No | No | Yes |
4장 priority Queue
▶Contents
- Binary Heap을 사용한 PQ의 구현
- Priority Queue 사용 애플리케이션 공통적인 특성
- Slider Puzzle and A* Search with PQ
▶Priority Queue
insert()
1. complete binary tree 형태를 유지한다.
2. heap order를 유지한다.
3. ~logN 시간에 새 원소를 추가한다.
insert(k)하는 새 값을 k라고 할 때, k를 tree 가장 마지막에(배열 끝에) 추가한다.
k를 부모 노드와 비교해 heap-order(부모 >= 자식) 어긴다면 swap 하는 것을 반복한다. (swim up)
(즉, heap-order 만족할 때까지 부모 노드 따라 계속 올라간다.)
index 0은 비워두고 1부터 담는다. -> 부모-자식 접근 식이 더 간단하다.
index 1부터 담기
Node i의 부모 : i // 2, 왼쪽 자식 : i * 2, 오른쪽 자식 : i * 2 + 1
index 0부터 담기
Node i의 부모 : (i - 1) // 2, 왼쪽 자식 : i * 2 + 1, 오른쪽 자식 : i * 2 + 2
class MaxHeap:
def __init__(self): # Constructor
self.pq = [''] # Empty key at pq[0]
def insert(self, key):
self.pq.append(key) # 새 원소 key를 배열 맨 끝에 추가
idx = len(self.pq)-1 # idx = 새 원소가 추가된 index
while idx>1 and self.pq[idx//2] < key: # 부모≥자식 조건 만족할 때까지 반복
self.pq[idx], self.pq[idx//2] = self.pq[idx//2], self.pq[idx] # key와 부모 swap
idx = idx//2 # key의 index를 부모가 있던 위치로 변경Q. insert() 비용은 ~logN으로 제한되는가?
A. ~lonN으로 제한된다. 왜냐하면 트리의 최대 깊이는 log2 N이기 때문이다.
가장 마지막 노드에 추가되어서 루트까지 올라간다 하더라도 log2 N만큼만 수행하기 때문이다.
delMax()
1. complete binary tree 형태를 유지한다.
2. heap order를 유지한다.
3. ~logN 시간에 max를 삭제한다.
root 값을 tree 가장 마지막 값 k와 swap 하며 배열에서 삭제한다.
k를 자식 노드 중 큰 쪽과 비교해 heap-order (부모 >= 자식) 어긴다면 swap 하는 것을 반복한다. (sink)
(즉, heap-order를 만족할 때까지 자식 노드 중 큰 쪽을 따라 계속 내려간다.
Q. delMax()할 때 root 삭제한 후, 자식 중 더 큰 쪽을 swim up 시키면 안 되는가?
A. 안된다. 큰 자식을 계속 올리다 보면,
어떤 경우에는 complete binary tree 형태를 유지할 수 없게 된다.
def delMax(self):
# root(max)와 마지막 원소 k swap
self.pq[1], self.pq[len(self.pq)-1] = self.pq[len(self.pq)-1], self.pq[1]
max = self.pq.pop() # 마지막에 있는 max 값 제거
idx = 1 # 마지막 원소 k가 있는 root에서 sink 시작
while 2*idx <= len(self.pq)-1: # 아래에 자식이 있다면 계속 sink 시도
idxChild = 2*idx
if idxChild<len(self.pq)-1 and self.pq[idxChild] < self.pq[idxChild+1]:
idxChild = idxChild+1 # 두 자식 중 더 큰 자식 찾기
if self.pq[idx] >= self.pq[idxChild]:
break # heap order 만족하면 sink 중단
# k와 더 큰 자식 swap함으로써 sink
self.pq[idx], self.pq[idxChild] = self.pq[idxChild], self.pq[idx]
idx = idxChild # k의 index를 자식이 있던 위치로 변경
return max
Heap 정리 : heap order 따라 원소를 배치하는 complete binary tree이다.
PQ의 효율적인 구현 방법이다.
(max) heap order : 부모 key >= 자식 key
따라서 어떤 노드라도 그 아래로 뻗어 나간 모든 노드 중 max, Delete(max 찾기)를 쉽게 한다.
complet binary tree
실제 트리를 만들지 않고, 배열을 사용해 편리하게 indexing이 가능하다.
트리 깊이 ~logN으로 제한해서 insert, delete 비용 또한 ~logN으로 제한된다.
| 구현방식 | insert() 비용 | delMin() 비용 |
| Unordered list | ~1 | ~N |
| Ordered array | ~N | ~1 |
| Binary Heap | ~log2 N | ~log2 N |
| d-ary Heap | ~logd N | ~d * logd N |
| 불가능 | ~1 | ~1 |
**Binay heap(complete binary tree)구조에서
Priority queue에 필요한 insert(), delMax() 효율적 수행 위해 (maxPQ 가정) Heap-order 조건 항상 만족하며 원소가 저장되도록 함
priority queue 기본 -> complete binary tree(이진트리 들어온 순서대로) 와 max heap order(부모key>=자식Key, 부모노드와비교해 swap함(swim up)) 사용 하여 시간복잡도를 낮춤 ~NlogN
insert , delMAX, delMIN
complete binary tree:사용이유
배열에 담으면 부모자식간 링크리스트 만들지 않아도 index만으로 배열에서 찾아갈수있음으로 메모리 절약 편리함
참고 index 0은 배열 비워두고 index 1부터 삽입 //만약 0부터 삽입하면 node i를 찾을때 부모i=(i-1),자식 +1씩 되어서 더복잡함
node i의
부모: i//2
왼쪽 자식: i×2
오른쪽 자식: i×2 + 1
Priority queue에 필요한 효율적 수행때문에 밑에 조건을 붙인다:
insert : 1. complete binary tree 형태 유지하며 2. heap order 유지하며 3. ~logN 시간에 max 삭제
delMax(): 1. complete binary tree 형태 유지하며 2. heap order 유지하며 3. ~logN 시간에 max 삭제
따라서 배열 맨끝에 insert 한 후에 delMax or delMin 젤위 노드 삭제 후 배열 젤끝에 애들 넣음 밑으로 내려가면서 대소 비교
따라서 배열에서 정렬을 사용한다면 PQ 사용해도 큰문제는 없다
배열정렬(오름차순 (혹은 내림차순)으로 원소 하나씩 꺼내 사용하기 위해)하는데 NlogN PQ 사용해도 logN작업을 N회 수행 따라서 NlogN동일
정렬된 배열에 insert 할때는 N^2이라서 차라리 PQ가 안전함 NlogN
정렬사용시 비용은 insert 1회비용 ~1 횟수N :~N
예시 slider puzzle3*3배열 ->시작점 목표지점까지 최단경로 찾기
A* search 구현 방법: 예측 이동 횟수 가장 작은 경우부터 우선 탐색하기 위해 Algorithm 2, Priority Queue
Min Priority Queue 사용
예측이동횟수 : depth+ (hamming vs manhattan) <= 실제 이동횟수
예상 문제
[Q] delMax()할 때 root 삭제한 후, 자식 중 더 큰 쪽을 swim up 시키는 것 반복하면 안되나? 왜 마지막 원소를 root에 두고 sink 시키나?
맨끝 node를 안올리면 대소비교가 깨져 순서가 엉망이됨 complete binary tree가 깨짐
1. (a*serach)minPQ에 남아있는 상태 :pop한 애 제외하고 밑에 갈수있는애들전부
2.다음에 pop되는 상태는 무엇인가 : 예측이동횟수가 젤 작은애 == 현재까지 이동횟수(depth)+mabhattan
조건 1,2를 항상 둘다 만족하기 힘듬
조건 1. 예측횟수가 실제 이도횟수에 가까울수록 불필요한 탐색을 줄일수있어 해를 빨리찾기가능(방법 두가지 hamming배열자리가맞는지개수 vs manhattan 배열이동횟수) ->최적에 가까운해 구할때 좋음
조건 2. 예측횟수<=실제이동횟수 조건을 만족해야 a*search 찾은 해가 최소이동횟수를 보장함 ->반드시 최적의 해를 구할때 좋음
'[CS] 컴퓨터 공학 > CS 수업 정리' 카테고리의 다른 글
| [데이터 베이스]7장 요약 (1) | 2023.10.29 |
|---|---|
| [수치해석] 중간 요약 (1) | 2023.10.27 |
| [데이터 베이스] ch7.Complex Queries, Triggers, Views, and Schema Modification (0) | 2023.10.17 |
| [데이터 베이스] ch6.Basic SQL (Structural Query Language) (1) | 2023.10.16 |
| 알고리즘 2 - Priority Queue (우선순위 큐) (0) | 2023.10.12 |

